Formulating one’s own nutrient solution should be left to advanced growers. Any mistake could lead to the loss of the whole crop, unless the mistake can be identified early, in which case the nutrient solution in the tank is lost.

The hypothetical example will be used to show how to calculate the amount of each fertilizers in order to make up the hypothetical nutrient formulation. Note that this formulation has been used by commercial growers, one should always adapt the ratio’s according your crop’s specifications as well as climate or environmental requirements.

A hypothetical nutrient formulation is could consist of the following concentrations:

A hypothetical nutrient solution which is used to explain how to formulate your own hydroponic nutrient solution. The concentrations can change but the basic method of how to calculate each element stays the same.

NutrientConcentration (mg.L-1
Nitrogen (N)200
Phosphorus (P)60
Potassium (K)300
Calcium (Ca)100
Magnesium (Mg)50
Sulphur (S)60
Iron (Fe)3
Boron (B)0.5
Manganese (Mn)0.2
Zinc (Zn)0.05
Copper (Cu)0.05
Molybdenum (Mo)0.5

The first question would be where to start and with what element. The following procedure should be followed. Always start with the element phosphorus and satisfy the required amount needed in the formulation. After phosphorus satisfy the calcium requirement and then the potassium requirements. By the time these elements requirements have been satisfied a large portion of the nitrogen and sulphur requirements will also be satisfied. Magnesium is the last macro element that should be satisfied. The micro elements should be done separately. If a complex is used, the calculation will be easy but if the micro elements are added as mono fertilizers, the calculation will be slightly longer but still quite straight forward.

The following procedure should be followed when calculating the amount of fertilizer to use in order to achieve a required concentration. We shall assume that a 1,000 L tank is to be used.




First solve for phosphorus

We select mono potassium phosphate (/ce{KH2PO4}). The molecular weight of mono potassium phosphate (MPP) is:

39 + (1 x 2) + 31 + (16 x 4) = 136

Next we calculate the amount of phosphorus per unit of MPP. We know there is 31/136×100 = 22.79% P in MPP (See How to calculate nutrient content with atomic weight and molecular weight). Each of the following statements are true:

There is 22.79 units of P in 100 units of MPP

There is 22.79 mg P in 100 mg MPP and

There is 22.79 mg.L-1 P in 100 mg.L-1 MPP

The last statement is exactly what we want, because we know the required amount of P is 60 mg.L-1 (as shown in the previous table). If we were to mix only 100 mg of MPP in 1 L, we would be short of 60-22.79 = 37.21 mg.L-1. Thus we would need to add more than 100 mg of MPP in one 1 L. For the moment we will be using only 1 L and later extrapolate it to 1,000 L. To determine how much MPP we need to make up a solution of 60 mg.L-1 P, we use the following principles:

We know there is 22.79 mg.L-1 P in 100 mg.L-1 MPP

We know there is 60.00 mg.L-1 P in X mg.L-1 MPP

The value of X is unknown and we must now solve the problem by using a simple linear mathematical ratio:

\dfrac{C_1}{C_2}\varpropto \dfrac{{C'}_1}{{C'}_2}

 Where the following applies

{C}_1} = Concentration of known element

{C}_2} = Concentration of known fertilizer

{C'}_1} = Concentration of required element

{C'}_2} = Concentration of unknown fertilizer

The sign  \varpropto =  means “equal in proportion” or ratio

The following values will be replaced in the formula:

{C}_1} = 22.79 mg.L-1 P

{C}_2} = 100 mg.L-1 MPP

{C'}_1} = 60.00 mg.L-1 P

{C'}_2} = X and we need to calculate this value

 By replacing all the values we have the following

\dfrac{22.79}{100.00}\varpropto \dfrac{60.00}{{C'}_2}

Thus, we need to solve for {C'}_2}

{C'}_2}=\dfrac{60 \times 100}{22.79}

{C'}_2}=263.27mg

Thus in order to have a concentration of 60 mg.L-1 P in the solution, we need to add 263.27 mg of MPP in 1 litre of water. But we do not have 1 litre of solution to make up, we have 1,000 L. Thus we have to multiply 263.27 by 1,000 = 263,270 mg of MPP needs to be added in 1,000 L of water. To make it more readable 263.27 mg is divided by 1,000 to convert to grams which is 263.27 g MPP. Thus we can say that 263.27 g of MPP will provide 60 mg.L-1 or 60 ppm of P in 1,000 L of water.

Now start solving for potassium (K)

We can clearly see that mono potassium phosphate (\ce{KH2PO4}) has potassium in the formula. Since we are adding 263.27 g of MPP to the nutrient solution, there will also be some potassium added. According to our nutrient formulation, we need 300 mg.L-1 K in the nutrient solution.

First we have to determine how much potassium is in mono potassium phosphate (\ce{KH2PO4}), then determine how much potassium has been added with the 263.27 g MPP and then we will have to determine how much of other potassium fertilizers we need to use to provide for the remaining K.

In order to determine how much K is in mono potassium phosphate (\ce{KH2PO4}) we use the atomic weight of K which is 39. The atomic weight of MPP is 136 as calculated earlier in  How to calculate nutrient content with atomic weight and molecular weight. We calculate the percentage of K in MPP which is 39/136X100 = 28.68 %. With this information we can state the following:

 There is 28.68 units of K in 100 units of MPP

There is 28.68 mg of K in 100 mg of MPP and

There is 28.68 mg.L-1 of K in 100 mg.L-1 MPP

Again we are were we would like to be since all units are in mg.L-1, which are the units in which the nutrient formulation are expressed. In order to determine how much K is in the amount of MPP that we added to the nutrient solution, we use the following principle:

 \dfrac{C_1}{C_2}\varpropto \dfrac{{C'}_1}{{C'}_2}

Where the following applies:

{C}_1} = Concentration of known element

{C}_2} = Concentration of known fertilizer

{C'}_1} = Concentration of required element

{C'}_2} = Concentration of unknown fertilizer

The sign  \varpropto =  means “equal in proportion” or ratio

The following values will be replaced in the formula:

{C}_1} = 28.68 mg.L-1 K

{C}_2} = 100 mg.L-1 MPP

{C'}_1} = X and we need to calculate this value which will be measured in mg.L-1

{C'}_2} = 263.27 mg.L-1 MMP

Remember in the previous example we had to calculate C’2 and in this case we need to calculate {C'}_1}. Previously we had to calculate the concentration of MPP which would provide a certain amount of P. In this case we know how much MPP we are added and would like to know how much K in added. By replacing all the values we have the following:

 \dfrac{28.68}{100.00}\varpropto \dfrac{{C'}_1}{263.27}

We need to solve for {C'}_1

 {C'}_1=\dfrac{28.68 \times 263.27}{100.00}

{C'}_1=75.51mg.L^{-1}K

 So, in the 263.27 mg.L-1 of MPP, there is 60 mg.L-1 of P and 75.51 mg.L-1 K. Remember this is expressed as a concentration. If we would like to know how much K was actually added in 1,000 L we need to determine how much K is in 263.27 g (grams) which is a thousand times more than 263.27 mg (milligram). So multiply the 75.51 mg by 1,000 would result in 75510 mg or 75.51 g. It sounds wrong but remember the units are not the same. The following equation will clarify why:

\dfrac{75.51mg}{1L}=\dfrac{84.51}{1000L}

Since we require 300 mg.L-1 of K in the nutrient solution, we are short of 300 – 75.51 = 224.49 mg.L-1. It is important not to solve the K requirement now since there are many fertilizers that can be used but each have other elements which will contribute to the nutrient formulation. After solving for P the next important element is calcium.

Now solve for calcium (Ca) and nitrogen (N):

There is only one fertilizer type to use and that is calcium nitrate. There are however two compounds; the granular type which is most commonly used and the liquid type. We will use the granular type. The nutrient formulation provided in the previous table (Hypothetical nutrient solution). requires 100 mg.L-1 of Calcium (Ca). The same procedure as followed with phosphorus should be followed to determine the amount of Calcium nitrate required to provide 100 mg.L-1 of Ca. The molecular weight of Calcium nitrate \ce{(Ca(NO3)2.4H2O})

40 + (2 x (14 + (16 x 3))+(4 x ( (1×2)+16) ) = 236

Next we calculate the amount of calcium per unit of calcium nitrate. We know there is 40/236×100 = 16.95 % Ca in Calcium nitrate. Each of the following statements are true:

There are 16.95 units of Ca in 100 units of calcium nitrate

There is 16.95 mg Ca in 100 mg calcium nitrate and

There is 16.95 mg.L-1 Ca in 100 mg.L-1 calcium nitrate

The last statement is exactly what we want, because we know the required amount of Ca is 100 mg.L-1. If we were to mix only 100 g of calcium nitrate in 1,000 L, we would be short of 100-16.95 = 83.05 mg.L-1 (Note the units have changed compared to calculating P) Thus we would need to add more than 100 g of calcium nitrate in one 1,000 L. To determine how much calcium nitrate we need to make up a solution of 100 mg.L-1 Ca, we use the following principles:

We know there is 16.95 mg.L-1 Ca in 100 mg.L-1 calcium nitrate

We know there is 16.95 mg.L-1 Ca in X mg.L-1 calcium nitrate

The value of X is unknown and we must now solve the problem by:

\dfrac{C_1}{C_2}\varpropto \dfrac{{C'}_1}{{C'}_2}

Where the following applies

C1 = Concentration of known element

C2 = Concentration of known fertilizer

C’1 = Concentration of required element

C’2 = Concentration of unknown fertilizer

\varpropto = the sign means “equal in proportion” or ratio

The following values will be replaced in the formula:

C1 = 16.95 mg.L-1 Ca

C2 = 100 mg.L-1 calcium nitrate

C’1 = 100.00 mg.L-1 Ca

C’2 = X and we need to calculate this value

By replacing all the values we have the following

\dfrac{C_1}{C_2}\varpropto \dfrac{{C'}_1}{{C'}_2}

\dfrac{16.95}{100} \varpropto \dfrac{100}{{C'}_2}

We need to solve for C'<sub>2</sub>

{C'}_2=\dfrac{100 \times 100}{16.95}

{C'}_2=589.97mg

Thus in order to have a concentration of 100 mg.L-1 Ca in the solution, we need to add 589.97 g calcium nitrate in 1,000 L of water.

We can clearly see that calcium nitrate (\ce{Ca(NO3)2.4H2O}) has not only calcium in the formula but nitrate as well. Since we are adding 589.97 g of calcium nitrate to the nutrient solution, there will also be some nitrates added. According to our nutrient formulation, we need 200 mg.L-1 N in the nutrient solution.

First we have to determine how much nitrogen is in calcium nitrate (\ce{Ca(NO3)2.4H2O}), then determine how much N has been added with the 589.97 g Calcium nitrate and then we will have to determine how much of other nitrogen fertilizers we need to use to provide for the remaining N.

In order to determine how much N is in calcium nitrate (\ce{Ca(NO3)2.4H2O}) we use the atomic weight of N which is 14. The atomic weight of calcium nitrate is 236 as calculated earlier in the chapter. We calculate the percentage of N in calcium nitrate which is 28/236X100 = 11.86 %. With this information we can state the following:

There is 11.86 units of N in 100 units of calcium nitrate

There is 11.86 mg of N in 100 mg of calcium nitrate and

There is 11.86 mg.L-1 of N in 100 mg.L-1 calcium nitrate

Again we are were we would like to be since all units are in mg.L-1, which are the units in which the nutrient formulation are expressed. In order to determine how much N is in the amount of calcium nitrate that we added to the nutrient solution, we use the following linear principle:

\dfrac{C_1}{C_2}\varpropto \dfrac{{C'}_1}{{C'}_2}

Where the following applies

C1 = Concentration of known element

C2 = Concentration of known fertilizer

C’1 = Concentration of required element

C’2 = Concentration of unknown fertilizer

\varpropto = the sign means “equal in proportion” or ratio

The following values will be replaced in the formula:

C1 = 11.86mg.L-1

C2 = 100 mg.L-1 calcium nitrate

C’1 = X and we need to calculate this value which will be measured in mg.L-1 N

C’2 = 589.97 mg.L-1 calcium nitrate (\ce{Ca(NO3)2.4H2O}) that we have added to the tank

 It should be clear now when to use C’1 and C’2. If not, go through the previous calculations again and try and figure it out. Briefly, C’1 is used when trying to calculate the concentration of an unknown nutrient and C’2 is used when the concentration of a fertilizer needs to be determined.

In this case we know how much calcium nitrate we are added and would like to know how much N is added as well.

By replacing all the values we have the following

\dfrac{11.86}{100} \varpropto \dfrac{{C'}_1}{589.97}

we need to solve for C’1

{C'}_1=\dfrac{11.86 \times 589.97}{100}

{C'}_1 = 69.97mg.l^{-1}

So, in the 589.97 mg.L-1 of calcium nitrate, there is 100 mg.L-1 of Ca and 69.97 mg.L-1 N. Remember this is expressed as a concentration. If we would like to know how much N was actually added in 1,000 L we need to determine how much N is in 589.97 g (grams) which is a thousand times more than 589.97 mg (milligram). So multiply the 35.00 mg by 1,000 would result in 69970 mg or 69.97 g. It sounds wrong but remember the units are not the same. The following equation will clarify why:

\dfrac{69.97mg}{1L} \varpropto \dfrac{69.97g}{1000L}

Since we require 200 mg.L-1 of N in the nutrient solution, we are short of 200 – 69.97 = 130.03 mg.L-1 N.

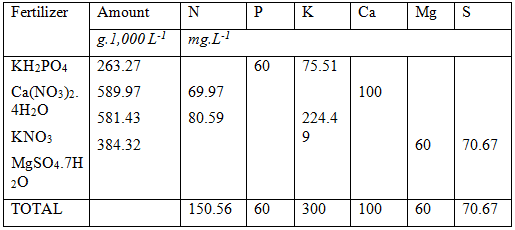
Up to now we have solved the following:

Phosphorus : 40 mg.L-1

Calcium : 100 mg. L-1

Potassium : 75.51 mg. L-1 (224.49 mg.L-1 more required)

Nitrogen ; 69.97 mg. L-1 (130.03 mg. L-1 more required)

 We still need to solve the remaining potassium and nitrogen requirements At this stage of the calculations it becomes slightly tricky. The remaining macro elements are N, K, Mg and S. The most common fertilizers that can be used for the remaining macro elements are: Potassium nitrate, Potassium sulphate, Magnesium Nitrate, Magnesium sulphate.

Each fertilizer will contribute to at least two nutrients. The problem is, if the wrong fertilizer is chosen first, for instance if potassium sulphide is used to satisfy the remaining K requirements, we might end up adding to much S in the solutions since there is S in potassium sulphide (\ce{K2SO4}). If however we use potassium nitrate (\ce{KNO3}), there might be to much N in the solution since potassium nitrate has both N and K in the formula. The safest method is to solve the remaining element with the lowest concentration i.e. magnesium then sulphate then nitrogen and lastly potassium. However this sequence does not always work and the final solution must be obtained through trial and error. The easiest is to use a linear programming tool found in many spreadsheet programs.




Now calculate magnesium (Mg) requirements:

The magnesium requirement will first be solved with magnesium sulphate (\ce{MgSO4.7H2O}) The aim with magnesium sulphide would be to satisfy the magnesium requirement first, then part of the sulphide content. The rest of the sulphide content will be made up from potassium sulphate, which will reduce the requirement of potassium. The rest of the nitrogen requirement will be satisfied with potassium nitrate and hopefully the potassium requirement will be satisfied.

We select magnesium sulphate (\ce{MgSO4.7H2O}). The molecular weight of magnesium sulphate is:

24 + 32 + (16 x 4) + (7 x ( (1×2) + 16) ) = 246

Next we calculate the amount of magnesium per unit of magnesium sulphate. We now there is 32/246×100 = 13.01 % Mg in magnesium sulphate. Each of the following statements is true:

There are 24 units of Mg in 100 units of magnesium sulphate1)Thank you for Jalil Aasayesh for noticing some errors in this calculation

There is 24 mg Mg in 100 mg magnesium sulphate and

There is 24 mg.L-1 P in 100 mg.L-1 magnesium sulphate

The last statement is exactly what we want, because we know the required amount of Mg is 50 mg.L-1. If we were to mix only 100 mg of magnesium sulphate in 1 L, we would be short of 50-24 = 26 mg.L-1. Thus we would need to add more than 100 mg of magnesium sulphate in one 1 L. To determine how much magnesium sulphate we need to make up a solution of 50 mg.L-1 Mg, we use the following principles:

We know there is 24 mg.L-1 Mg in 100 mg.L-1 magnesium sulphate

We know there is 50 mg.L-1 Mg in X mg.L-1 magnesium sulphate

The value of X is unknown and we must now solve the problem by using a simple linear mathematical ratio:

\dfrac{C_1}{C_2}\varpropto \dfrac{{C'}_1}{{C'}_2}

Where the following applies

C1 = Concentration of known element

C2 = Concentration of known fertilizer

C’1 = Concentration of required element

C’2 = Concentration of unknown fertilizer

\varpropto = the sign means “equal in proportion” or ratio

The following values will be replaced in the formula:

C1 = 24 mg.L-1 Mg

C2 = 100 mg.L-1 magnesium sulphate

C’1 = 50.00 mg.L-1 Mg

C’2 = X and we need to calculate this value

By replacing all the values we have the following

\dfrac{24}{100} \varpropto \dfrac{50}{{C'}_2}

{C'}_2=\dfrac{50 \times 100}{24}

{C'}_2=357.14g.1000L^{-1}

Thus in order to have a concentration of 50 mg.L-1 Mg in the solution, we need to add 357.14 g of magnesium sulphate in 1,000 litre of water.

Magnesium sulphate contains both magnesium and sulphate (S). We have to determine how much S will be added to the solution through the 357.14 g of magnesium sulphate.

First we have to determine how much sulphide is in magnesium sulphate (\ce{MgSO4.7H2O}), then determine how much S has been added with the 357.14 g of magnesium sulphate and then we will have to determine how much of other sulphide fertilizers we need to use to provide for the remaining sulphate.

In order to determine how much S is in magnesium sulphate (\ce{MgSO4.7H2O}) we use the atomic weight of S which is 32. The atomic weight of magnesium sulphate is 246 as calculated earlier in the chapter. We calculate the percentage of S in magnesium sulphate which is 32/246×100 = 13.01 %. With this information we can state the following:

 There are 13.01 units of S in 100 units of magnesium sulphate

There is 13.01 mg of S in 100 mg of magnesium sulphate and

There is 13.01 mg.L-1 of S in 100 mg.L-1 magnesium sulphate

Again we are where we would like to be since all units are in mg.L-1, which are the units in which the nutrient formulation are expressed. In order to determine how much S is in the amount of magnesium sulphate that we added to the nutrient solution, using a simple linear mathematical ratio:

\dfrac{C_1}{C_2}\varpropto \dfrac{{C'}_1}{{C'}_2}

Where the following applies

C1 = Concentration of known element

C2 = Concentration of known fertilizer

C’1 = Concentration of required element

C’2 = Concentration of unknown fertilizer

\varpropto = The sign means “equal in proportion” or ratio

The following values will be replaced in the formula:

C1 = 13.01 mg.L-1 S

C2 = 100 mg.L-1 magnesium sulphate

C’1 = X and we need to calculate this value which will be measured in mg.L-1 N

C’2 = 357.14 mg.L-1 magnesium sulphate that we have added to the tank

By replacing all the values we have the following

\dfrac{18.39}{100} \varpropto \dfrac{{C'}_1}{384.32}

We need to solve for C’1:

{C'}_1=\dfrac{13.01 \times 357.14}{100}

C’1=46.46mg.L-1

So, in the 357.14 mg.L-1 of magnesium sulphate, there is 50 mg.L-1 of Mg and 46.46 mg.L-1 S. According to the nutrient formulation required in the previous table, we require 60 mg.L-1 S. The absolute difference of [60-51.61] = 13.54 mg.L-1 S will have no significant influence on the formulation2)There are many other Sulphur sources from various fertilizers being used simultaneously in making up solutions, so don’t worry too much about it..

We now have to complete the macro element requirements for nitrogen and potassium using potassium nitrate. The atomic weight of potassium nitrate is 39 + 14 + (16 x 3) = 101. The complete procedure will not be explained in detail as in previous examples, but a new problem that arises will be discussed. We can either solve for the remaining potassium requirement or the remaining nitrogen requirement. Lets see which is the worst of the two evils.

According to the calculations we need 224.49 mg.L-1 K and 165.00 mg. L-1 N. There is 39/101×100=38.61 % K in \ce{KNO3} and 14/101×100=13.86 % N in \ce{KNO3}.

Option 1: (Solving for K)

There is 38.61 mg.L-1 K in 100 mg.L-1\ce{KNO3}

There is 224.49 mg.L-1 K in 581.43 mg.L-1 \ce{KNO3}

The total amount of K in the nutrient solution is 75.51 mg.L-1 added through \ce{KH2PO4} and 224.49 mg.L-1 added through\ce{KNO3}. That totals 300 mg.L-1 which is exactly what the hypothetical nutrient solution requires.

If 581.43 g \ce{KNO3} is added to a 1,000 L tank the amount of N will be 581.43 mg.L-1×13.86 % = 80.59 mg.L-1 N. Thus we are 130.03– 80.59 = 49.44 mg. L-1 N short and must supply N in another form.

Option 2: (Solving for N)

There is 13.86 mg.L-1 N in 100 mg.L-1 \ce{KNO3}

There is 164.91 mg.L-1 N in 1189.83 mg.L-1 \ce{KNO3}

If 1189.83 g \ce{KNO3} is added to a 1,000 L tank the amount of K will be 1189.83 mg.L-1 × 38.61 % = 459.40 mg.L-1 K. Thus we are 459.40 – 224.49 = 234.91 mg. L-1 K in excess. This option is not viable so we will stay with option 1.

Up to this point we have satisfied all nutrients except nitrogen of which there is 49.44 mg.L-1 required. However, all fertilizers that contain nitrogen have either potassium, magnesium or calcium as well. Using any of these fertilizers would increase another element as well.

fertilizer hydroponic nutrient formulations

Total amount of fertilizers used to solve the hypothetical nutrient solution

There is one fertilizer that we have not used yet, and that is ammonium nitrate. The golden rule is never to use more than 5 % of the total N requirement as ammonium since it can burn the root system and affect the uptake of Ca negatively causing physiological disorders such as blossom-end-rot with tomatoes. The maximum allowed is 5 % of 200 mg.L-1 which is 10 mg.L-1. The formula for ammonium nitrate is \ce{NH4NO3}.

/ce{NH4NO3}: MW = 80; N = 35.00 %

35.00 mg.L-1 N in 100 mg.L-1 \ce{NH4NO3}

10.00 mg.L-1 N in X mg.L-1 \ce{NH4NO3}

X = (10 × 100)/35.00 = 28.57 mg.L-1 \ce{NH4NO3}

We now require 49.44-10=39.44 mg.L-1 N. The only fertilizer that we can increase is \ce{Ca(NO3)2.4H2O}. The hypothetical formulation requires 100 mg.L-1 Ca but it can easily be increased to at least 160 mg.L-1 without harming the plants. In any case, since we have increased the Mg content from 50 mg.L-1 to 60 mg.L-1, it would be better for the Ca:Mg ratio in the nutrient solution to increase the Ca content of the solution slightly. We require an additional 70.59 mg.L-1 N and will be provided by \ce{Ca(NO3)2.4H2O}.

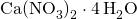  • \ce{Ca(NO3)2.4H2O}: MW = 236; Ca = 16.95 % ;N = 11.86 %
  • 11.86 mg.L-1 N in 100 mg.L-1 \ce{Ca(NO3)2.4H2O}
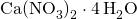
  • 49.44 mg.L-1 N in X mg.L-1 \ce{Ca(NO3)2.4H2O}
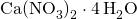
  • X = (49.44 x 100)/11.86 = 416.86 mg.L-1 \ce{Ca(NO3)2.4H2O}
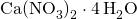
  • Extra Ca in 416.86 mg.L-1 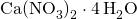\ce{Ca(NO3)2.4H2O} is:
  • 416.86 x 16.95 % = 70.66 mg.L-1 N

The increase in Ca content in the nutrient solution to 170.66 mg.L-1 is acceptable. Some researchers have even recommended concentrations of up to 200 mg.L-1 Ca. For instance the well known Hoagland solution has a Ca concentration between 160 and 200 mg.L-1, with the Mg content varying between 50 and 100 mg.L-1.

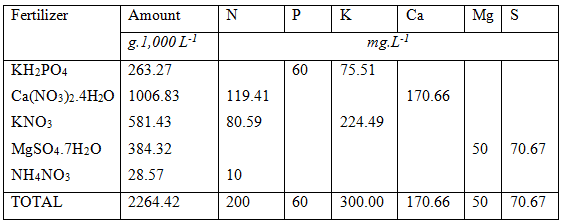
After all these calculations the final list of fertilizers used are listed below. It evident that the calculation of nutrient formulation is no easy task. The easiest way to obtain the right answer fast is to use a spreadsheet application that can be automated or use complex fertilizers.

hydroponic nutrinet solutions

Total amount of fertilizers used to solve the hypothetical nutrient solution

It is possible to obtain the required hypothetical nutrient formulation with other fertilizers such as Calcium Magnesium Nitrate Plus, Potassium Carbonate, Mono-potassium Phosphate, Potassium Sulphate, Urea, MAP and DAP. and other water soluble fertilizers in the form of 5:1:5(37), 6:1:4(31) and 3:1:2(36). Some of these fertilizers are not very soluble in water and have to be mixed in hot water first.

References

References
↑1 Thank you for Jalil Aasayesh for noticing some errors in this calculation
↑2 There are many other Sulphur sources from various fertilizers being used simultaneously in making up solutions, so don’t worry too much about it.